Equal Area Cylindrical¶
Classification |
Cylindrical |
Available forms |
Forward and inverse, spherical and ellipsoidal |
Defined area |
Global |
Alias |
cea |
Domain |
2D |
Input type |
Geodetic coordinates |
Output type |
Projected coordinates |
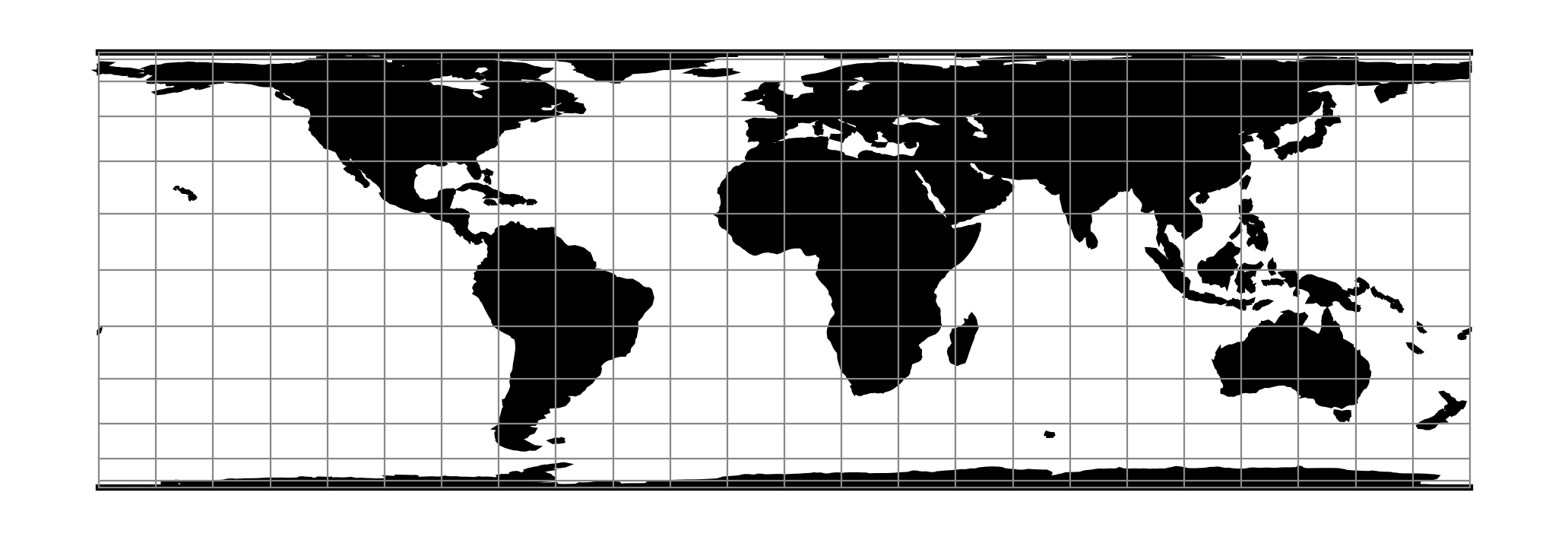
proj-string: +proj=cea¶
Named specializations¶
The Equal Area Cylindrical projection is sometimes known under other names when
it is instantiated with particular values of the lat_ts parameter:
Name |
lat_ts |
Lambert cylindrical equal-area |
0 |
Behrmann |
30 |
Gall-Peters |
45 |
Parameters¶
Note
All parameters are optional for the Equal Area Cylindrical projection.
- +lat_ts=<value>¶
Latitude of true scale. Defines the latitude where scale is not distorted. Takes precedence over
+k_0if both options are used together.Defaults to 0.0.
Note
The default convention is to interpret this value as decimal degrees. To specify radians instead, follow the value with the "r" character.
Example: +lat_ts=1.570796r
See Projection Units for more information.
- +lon_0=<value>¶
Central meridian/longitude of natural origin, longitude of origin or longitude of false origin (naming and meaning depend on the projection method).
Defaults to 0.0.
Note
The default convention is to interpret this value as decimal degrees. To specify radians instead, follow the value with the "r" character.
Example: +lon_0=1.570796r
See Projection Units for more information.
- +ellps=<value>¶
The name of a built-in ellipsoid definition.
See Ellipsoids for more information, or execute
proj -lefor a list of built-in ellipsoid names.Defaults to "GRS80".
- +R=<value>¶
Radius of the sphere, given in meters. If used in conjunction with
+ellps,+Rtakes precedence.See Ellipsoid size parameters for more information.
- +k_0=<value>¶
Scale factor. Determines scale factor used in the projection.
Defaults to 1.0.
- +x_0=<value>¶
False easting, easting at false origin or easting at projection centre (naming and meaning depend on the projection method). Always in meters.
Defaults to 0.0.
- +y_0=<value>¶
False northing, northing at false origin or northing at projection centre (naming and meaning depend on the projection method). Always in meters.
Defaults to 0.0.
Note
lat_ts and k_0 are mutually exclusive. If lat_ts
is specified, it is equivalent to setting k_0 to
\(\frac{\cos \phi_{ts}}{\sqrt{1 - e^2 \sin^2 \phi_{ts}}}\)