Ellipsoids¶
An ellipsoid is a mathematically defined surface which approximates the geoid: the surface of the Earth's gravity field, which is approximately the same as mean sea level.
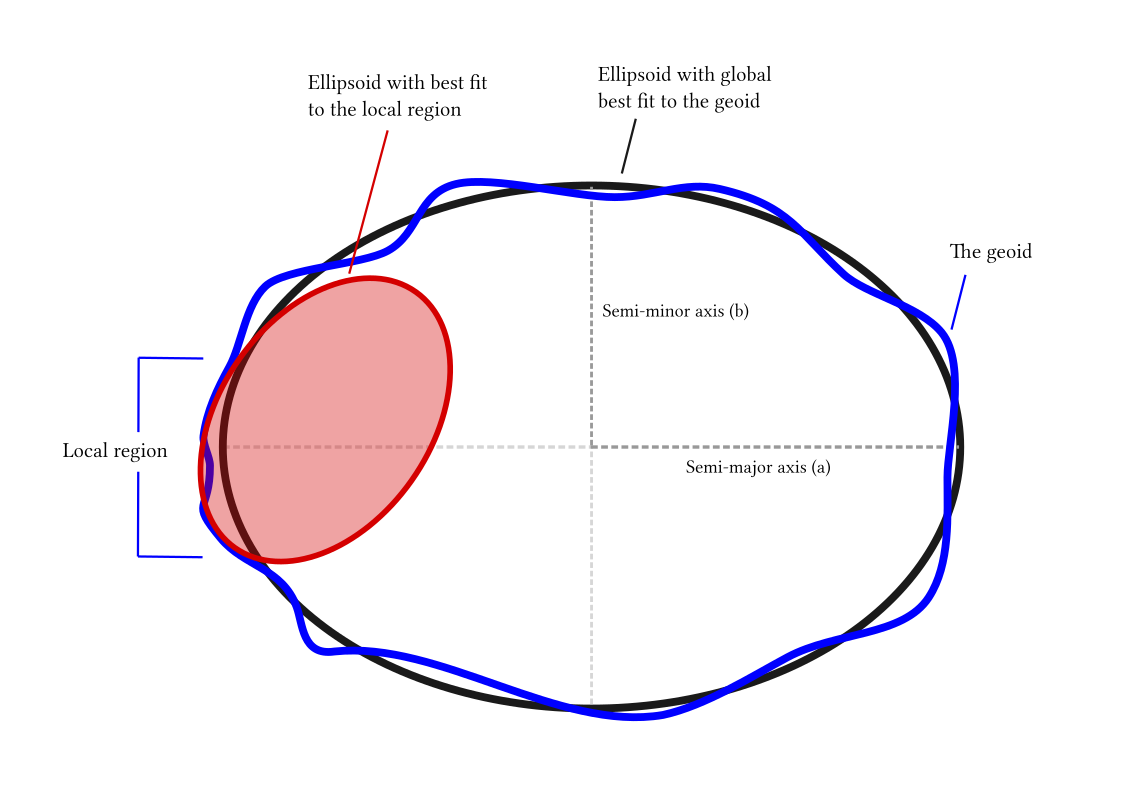
Global and local fitting of the ellipsoid¶
A complete ellipsoid definition comprises a size (primary) and a shape (secondary) parameter.
Ellipsoid size parameters¶
- +R=<value>¶
Radius of the sphere, \(R\).
- +a=<value>¶
Semi-major axis of the ellipsoid, \(a\).
Ellipsoid shape parameters¶
- +rf=<value>¶
Reverse flattening of the ellipsoid, \(1/f\).
- +f=<value>¶
Flattening of the ellipsoid, \(f\).
- +es=<value>¶
Eccentricity squared, \(e^2\).
- +e=<value>¶
Eccentricity, \(e\).
- +b=<value>¶
Semi-minor axis, \(b\).
The ellipsoid definition may be augmented with a spherification flag, turning the ellipsoid into a sphere with features defined by the ellipsoid.
Ellipsoid spherification parameters¶
- +R_A¶
A sphere with the same surface area as the ellipsoid.
- +R_V¶
A sphere with the same volume as the ellipsoid.
- +R_C¶
Added in version 9.3.0.
A sphere whose radius is the radius of the conformal sphere at \(\phi_0\).
- +R_a¶
A sphere with \(R = (a + b)/2\) (arithmetic mean).
- +R_g¶
A sphere with \(R = \sqrt{ab}\) (geometric mean).
- +R_h¶
A sphere with \(R = 2ab/(a+b)\) (harmonic mean).
- +R_lat_a=<phi>¶
A sphere with \(R\) being the arithmetic mean of the corresponding ellipsoid at latitude \(\phi\).
- +R_lat_g=<phi>¶
A sphere with \(R\) being the geometric mean of the corresponding ellipsoid at latitude \(\phi\).
If +R is given as size parameter, any shape and spherification
parameters given are ignored.
Built-in ellipsoid definitions¶
The +ellps=xxx parameter provides both size and shape for a number of
built-in ellipsoid definitions. Default is GRS80 if not given.
ellps
Parameters
Datum name
GRS80
a=6378137.0 rf=298.257222101
GRS 1980(IUGG, 1980)
airy
a=6377563.396 b=6356256.910
Airy 1830
bessel
a=6377397.155 rf=299.1528128
Bessel 1841
clrk66
a=6378206.4 b=6356583.8
Clarke 1866
intl
a=6378388.0 rf=297.
International 1909 (Hayford)
WGS60
a=6378165.0 rf=298.3
WGS 60
WGS66
a=6378145.0 rf=298.25
WGS 66
WGS72
a=6378135.0 rf=298.26
WGS 72
WGS84
a=6378137.0 rf=298.257223563
WGS 84
sphere
a=6370997.0 b=6370997.0
Normal Sphere (r=6370997)
If size and shape are given as +ellps=xxx, later shape and size parameters
are are taken into account as modifiers for the built-in ellipsoid definition.
While this may seem strange, it is in accordance with historical PROJ
behavior. It can e.g. be used to define coordinates on the ellipsoid
scaled to unit semimajor axis by specifying +ellps=xxx +a=1
Transformation examples¶
Spherical earth with radius 7000km:
+proj=latlon +R=7000000
Using the GRS80 ellipsoid:
+proj=latlon +ellps=GRS80
Expressing ellipsoid by semi-major axis and reverse flattening (\(1/f\)):
+proj=latlon +a=6378137.0 +rf=298.25
Spherical earth based on volume of ellipsoid
+proj=latlon +a=6378137.0 +rf=298.25 +R_V