Central Conic¶
Added in version 5.0.0.
This is central (centrographic) projection on cone tangent at :option:lat_1
latitude, identical with conic() projection from mapproj R package.
Classification |
Conic |
Available forms |
Forward and inverse, spherical projection |
Defined area |
Global, but best used near the standard parallel |
Alias |
ccon |
Domain |
2D |
Input type |
Geodetic coordinates |
Output type |
Projected coordinates |
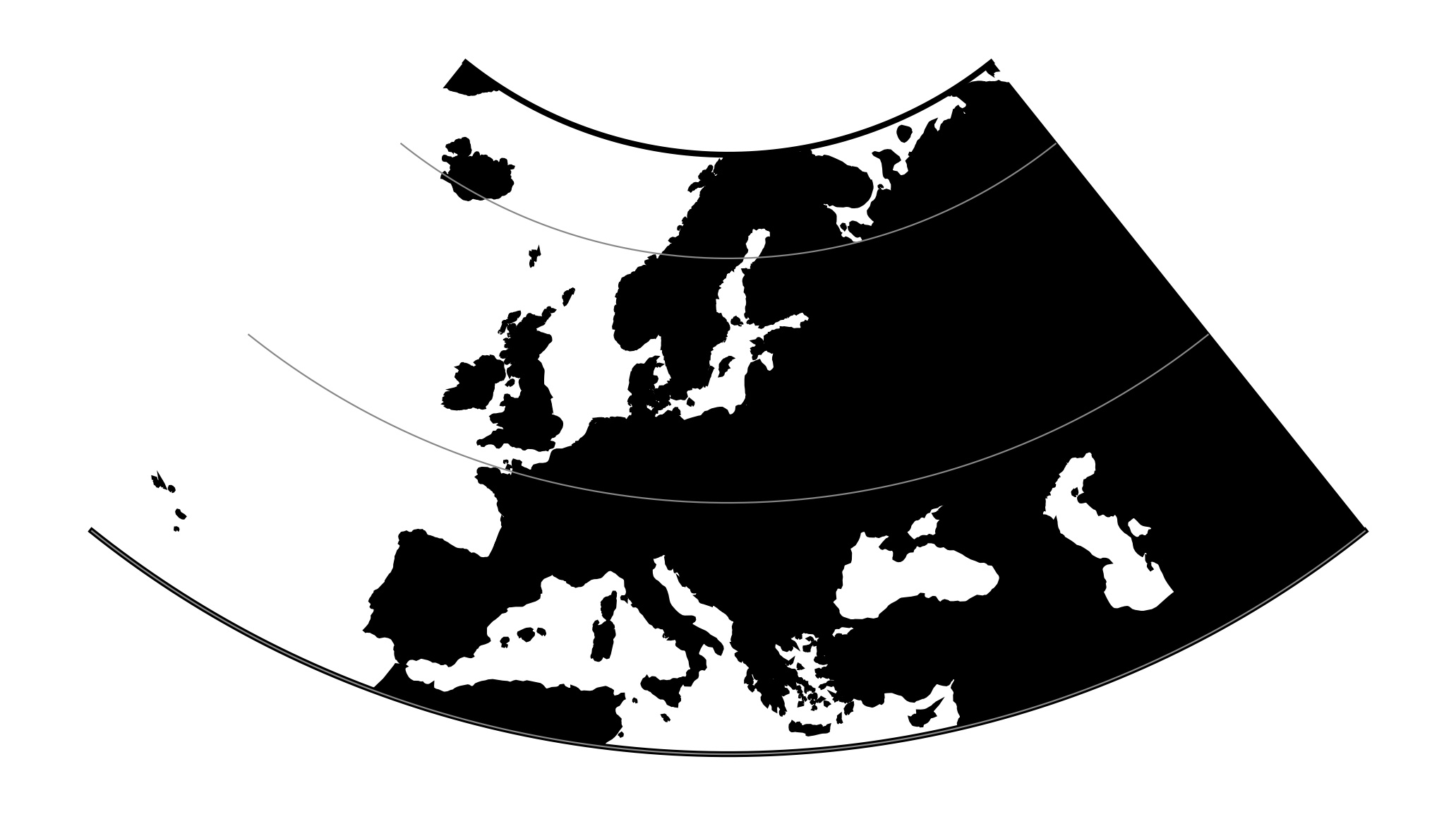
proj-string: +proj=ccon +lat_1=52 +lon_0=19¶
Usage¶
This simple projection is rarely used, as it is not equidistant, equal-area, nor conformal.
An example of usage (and the main reason to implement this projection in proj4) is the ATPOL geobotanical grid of Poland, developed in Institute of Botany, Jagiellonian University, Krakow, Poland in 1970s [Zajac1978]. The grid was originally handwritten on paper maps and further copied by hand. The projection (together with strange Earth radius) was chosen by its creators as the compromise fit to existing maps during first software development in DOS era. Many years later it is still de facto standard grid in Polish geobotanical research.
The ATPOL coordinates can be achieved with with the following parameters:
+proj=ccon +lat_1=52 +lon_0=19 +axis=esu +a=6390000 +x_0=330000 +y_0=-350000
For more information see [Komsta2016] and [Verey2017].
Parameters¶
Required¶
- +lat_1=<value>¶
Standard parallel of projection.
Optional¶
- +lon_0=<value>¶
Central meridian/longitude of natural origin, longitude of origin or longitude of false origin (naming and meaning depend on the projection method).
Defaults to 0.0.
Note
The default convention is to interpret this value as decimal degrees. To specify radians instead, follow the value with the "r" character.
Example: +lon_0=1.570796r
See Projection Units for more information.
- +R=<value>¶
Radius of the sphere, given in meters. If used in conjunction with
+ellps,+Rtakes precedence.See Ellipsoid size parameters for more information.
- +x_0=<value>¶
False easting, easting at false origin or easting at projection centre (naming and meaning depend on the projection method). Always in meters.
Defaults to 0.0.
- +y_0=<value>¶
False northing, northing at false origin or northing at projection centre (naming and meaning depend on the projection method). Always in meters.
Defaults to 0.0.
Mathematical definition¶
Forward projection¶
Inverse projection¶
Reference values¶
For ATPOL to WGS84 test, run the following script:
#!/bin/bash
cat << EOF | src/cs2cs -v -f "%E" +proj=ccon +lat_1=52 +lat_0=52 +lon_0=19 +axis=esu +a=6390000 +x_0=330000 +y_0=-350000 +to +proj=longlat
0 0
0 700000
700000 0
700000 700000
330000 350000
EOF
It should result with
1.384023E+01 5.503040E+01 0.000000E+00
1.451445E+01 4.877385E+01 0.000000E+00
2.478271E+01 5.500352E+01 0.000000E+00
2.402761E+01 4.875048E+01 0.000000E+00
1.900000E+01 5.200000E+01 0.000000E+00
Analogous script can be run for reverse test:
cat << EOF | src/cs2cs -v -f "%E" +proj=longlat +to +proj=ccon +lat_1=52 +lat_0=52 +lon_0=19 +axis=esu +a=6390000 +x_0=330000 +y_0=-350000
24 55
15 49
24 49
19 52
EOF
and it should give the following results:
6.500315E+05 4.106162E+03 0.000000E+00
3.707419E+04 6.768262E+05 0.000000E+00
6.960534E+05 6.722946E+05 0.000000E+00
3.300000E+05 3.500000E+05 0.000000E+00