Oblique Mercator¶
The Oblique Mercator projection is a cylindrical map projection that closes the gap between the Mercator and the Transverse Mercator projections.
Classification |
Conformal cylindrical |
Available forms |
Forward and inverse, spherical and ellipsoidal |
Defined area |
Global, but reasonably accurate only within 15 degrees of the oblique central line |
Alias |
omerc |
Domain |
2D |
Input type |
Geodetic coordinates |
Output type |
Projected coordinates |
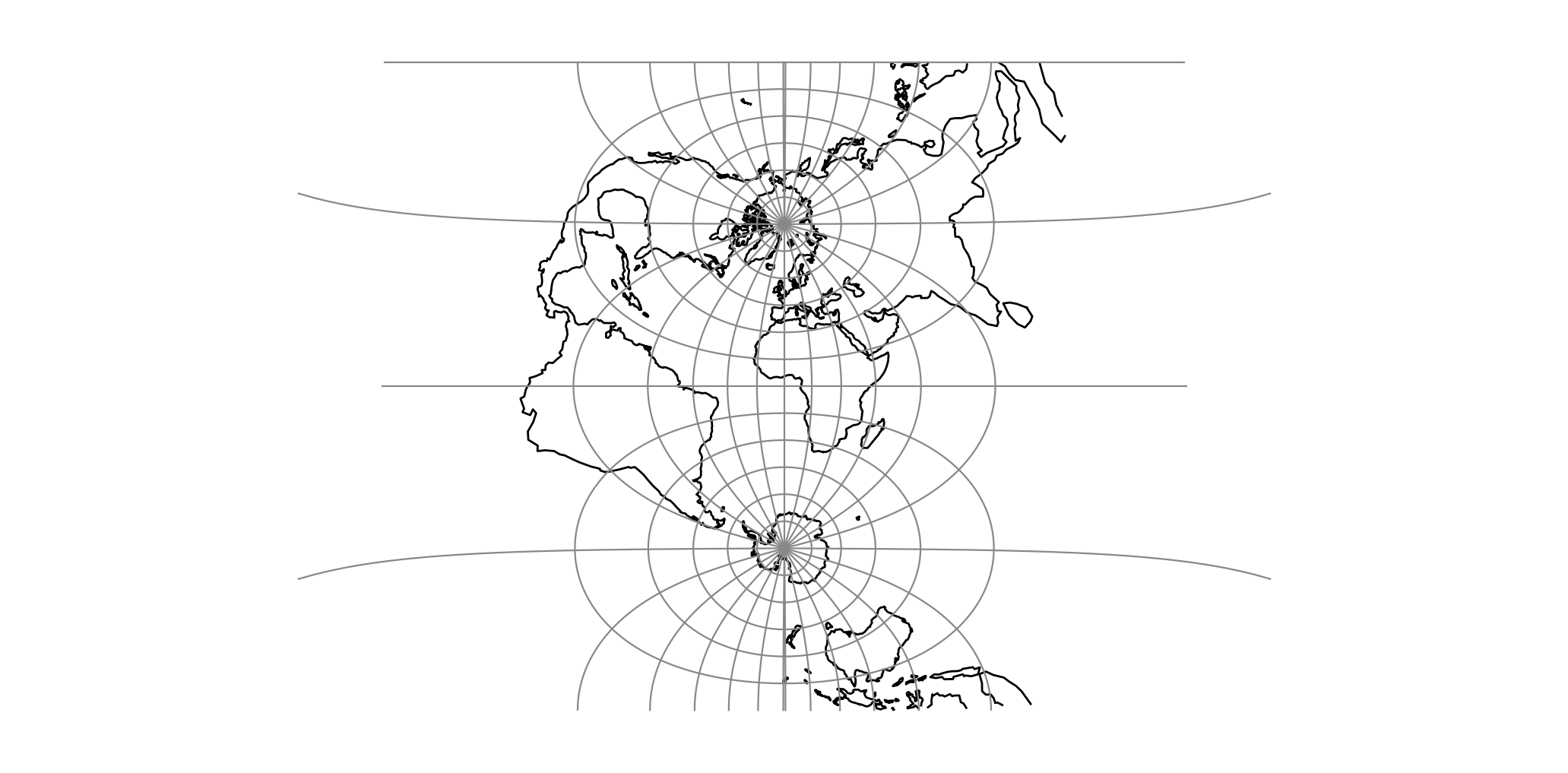
proj-string: +proj=omerc +lat_1=45 +lat_2=55¶
Figuratively, the cylinder used for developing the Mercator projection touches the planet along the Equator, while that of the Transverse Mercator touches the planet along a meridian, i.e. along a line perpendicular to the Equator.
The cylinder for the Oblique Mercator, however, touches the planet along a line at an arbitrary angle with the Equator. Hence, the Oblique Mercator projection is useful for mapping areas having their greatest extent along a direction that is neither north-south, nor east-west.
The Mercator and the Transverse Mercator projections are both limiting forms of the Oblique Mercator: The Mercator projection is equivalent to an Oblique Mercator with central line along the Equator, while the Transverse Mercator is equivalent to an Oblique Mercator with central line along a meridian.
For the sphere, the construction of the Oblique Mercator projection can be imagined as "tilting the cylinder of a plain Mercator projection", so the cylinder, instead of touching the equator, touches an arbitrary great circle on the sphere. The great circle is defined by the tilt angle of the central line, hence putting land masses along that great circle near the centre of the map, where the Equator would go in the plain Mercator case.
The ellipsoidal case, developed by Hotine, and refined by Snyder [Snyder1987] is more complex, involving initial steps projecting from the ellipsoid to another curved surface, the "aposphere", then projection from the aposphere to the skew uv-plane, before finally rectifying the skew uv-plane onto the map XY plane.
Usage¶
The tilt angle (azimuth) of the central line can be given in two different ways.
In the first case, the azimuth is given directly, using the option +alpha
and defining the centre of projection using the options +lonc and
+lat_0.
In the second case, the azimuth is given indirectly by specifying two points on
the central line, using the options
+lat_1, +lon_1, +lat_2, and +lon_2.
Example: Verify that the Mercator, and Transverse Mercator (on a sphere), projections are limiting forms of the Oblique Mercator
$ echo 12 55 | proj +proj=merc +ellps=GRS80
1335833.89 7326837.71
$ echo 12 55 | proj +proj=omerc +alpha=90 +ellps=GRS80
1335833.89 7326837.71
$ echo 12 55 | proj +proj=omerc +alpha=0 +R=6400000
766869.97 6209742.96
# Same, with azimuth given indirectly via two points:
$ echo 12 55 | proj +proj=omerc +lon_1=0 +lat_1=-1 +lon_2=0 +lat_2=0 +R=6400000
766869.97 6209742.96
$ echo 12 55 | proj +proj=tmerc +R=6400000
766869.97 6209742.96
Example: Second case - indirectly given azimuth
$ echo 12 55 | proj +proj=omerc +lon_1=-1 +lat_1=1 +lon_2=0 +lat_2=0 +ellps=GRS80
349567.57 6839490.50
# Same, with directly given azimuth, (via: echo 0 0 1 -1|geod -I -f %.7f +ellps=GRS80):
$ echo 12 55 | proj +proj=omerc +alpha=-45.1880402 +ellps=GRS80
349567.57 6839490.50
Example: An approximation of the Danish "System 34" from [Rittri2012]
$ echo 10.536498003 56.229892362 | cs2cs +proj=longlat +ellps=GRS80 +to +proj=omerc +axis=wnu +lonc=9.46 +lat_0=56.13333333 +x_0=-266906.229 +y_0=189617.957 +k=0.9999537 +alpha=-0.76324 +gamma=0 +ellps=GRS80
200000.13 199999.89
The input coordinate represents the System 34 datum point "Agri Bavnehoj", with coordinates (200000, 200000) by definition. So at the datum point, the approximation is off by about 17 cm. This use case represents a datum shift from a cylinder projection on an old, slightly misaligned datum, to a similar projection on a modern datum.
Parameters¶
Central point and azimuth method¶
- +alpha=<value>¶
Azimuth of centerline clockwise from north at the center point of the line. If
+gammais not given then+alphadetermines the value of+gamma.
- +gamma=<value>¶
Azimuth of centerline clockwise from north of the rectified bearing of centre line. If
+alphais not given, then+gammais used to determine+alpha.If specifying only
+gammawithout+alpha, the maximum value of the absolute value of+gammais a function of the absolute value of+lat_0, equal to \(90° - |\phi_0|\) on a sphere and slightly above on a non-spherical ellipsoid.
- +lonc=<value>¶
Longitude of the projection centre. Note that this value is used to override the
+lon_0parameter, so the latter should not be specified as it would get ignored.
- +lat_0=<value>¶
Latitude of the projection centre.
Two point method¶
- +lon_1=<value>¶
Longitude of first point.
- +lat_1=<value>¶
Latitude of first point.
- +lon_2=<value>¶
Longitude of second point.
- +lat_2=<value>¶
Latitude of second point.
Optional¶
- +no_rot¶
No rectification (not "no rotation" as one may well assume). Do not take the last step from the skew uv-plane to the map XY plane.
Note
This option is probably only marginally useful, but remains for (mostly) historical reasons.
- +no_off¶
Do not offset origin to center of projection.
- +k_0=<value>¶
Scale factor. Determines scale factor used in the projection.
Defaults to 1.0.
- +x_0=<value>¶
False easting, easting at false origin or easting at projection centre (naming and meaning depend on the projection method). Always in meters.
Defaults to 0.0.
- +y_0=<value>¶
False northing, northing at false origin or northing at projection centre (naming and meaning depend on the projection method). Always in meters.
Defaults to 0.0.
Caveats¶
Note for the two-point method no rectification is done,
echo 0 0|proj -I +proj=omerc +R=6400000 +lonc=-87 +lat_0=42 +alpha=0
87dW 42dN
echo 0 0|proj -I +proj=omerc +R=6400000 +lonc=-87 +lat_0=42 +alpha=0 +no_rot
87dW 0dS
echo 0 0|proj -I +proj=omerc +R=6400000 +lon_1=-87 +lat_1=42 +lon_2=-87 +lat_2=43
87dW 0dN
Thus, just as was noted above regarding +no_rot, the two-point method itself is also probably only marginally useful.