Tobler-Mercator¶
Added in version 6.0.0.
Equal area cylindrical projection with the same latitudinal spacing as Mercator projection.
Classification |
Cylindrical equal area |
Available forms |
Forward and inverse, spherical only |
Defined area |
Global, conventionally truncated at about 80 degrees north and south |
Alias |
tobmerc |
Domain |
2D |
Input type |
Geodetic coordinates |
Output type |
Projected coordinates |
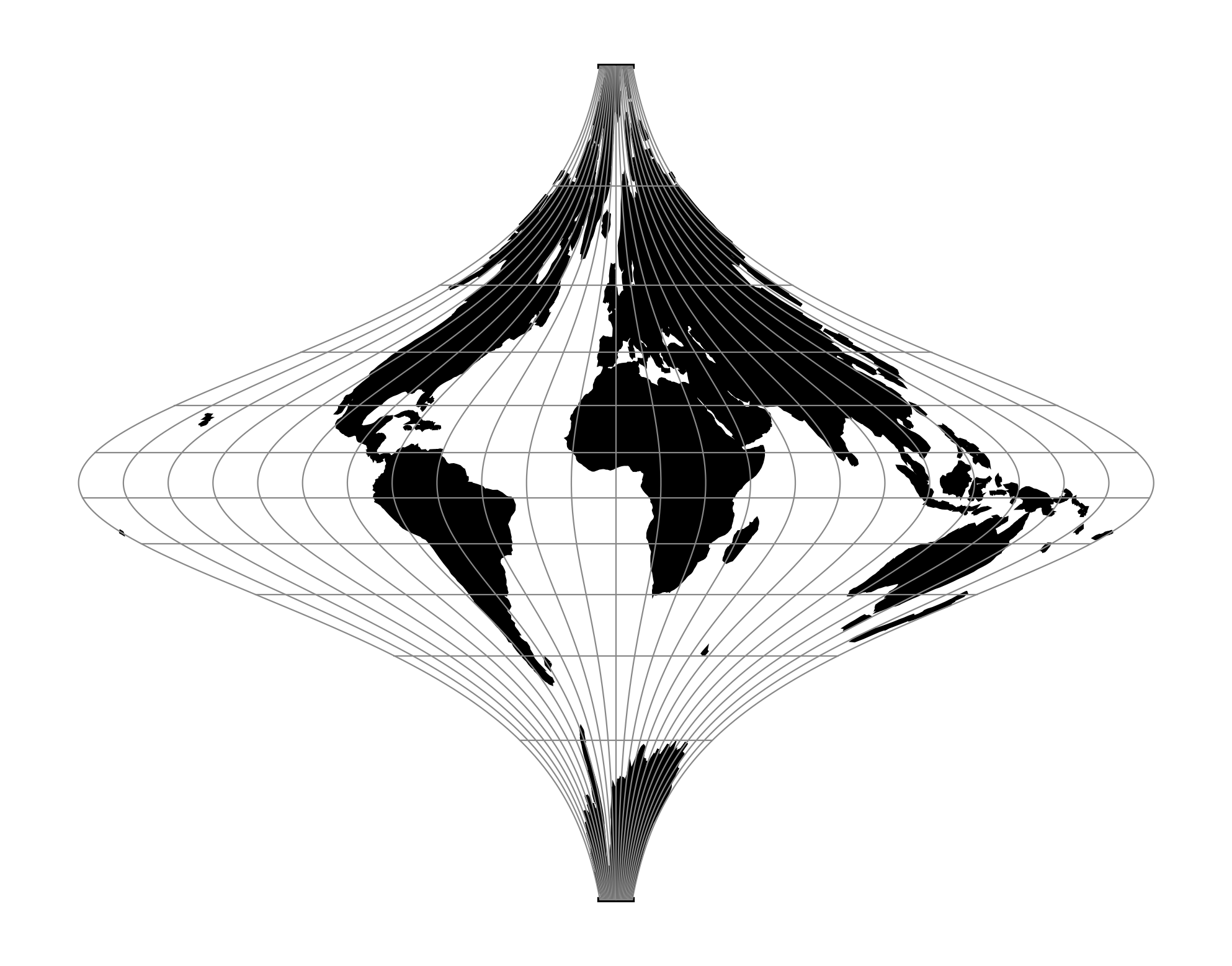
proj-string: +proj=tobmerc¶
Usage¶
The inappropriate use of the Mercator projection has declined but still occasionally occurs. One method of contrasting the Mercator projection is to present an alternative in the form of an equal area projection. The map projection derived here is thus not simply a pretty Christmas tree ornament: it is instead a complement to Mercator's conformal navigation anamorphosis and can be displayed as an alternative. The equations for the new map projection preserve the latitudinal stretching of the Mercator while adjusting the longitudinal spacing. This allows placement of the new map adjacent to that of Mercator. The surface area, while drastically warped, maintains the correct magnitude.
Parameters¶
Note
All parameters for the projection are optional.
- +k_0=<value>¶
Scale factor. Determines scale factor used in the projection.
Defaults to 1.0.
- +lon_0=<value>¶
Central meridian/longitude of natural origin, longitude of origin or longitude of false origin (naming and meaning depend on the projection method).
Defaults to 0.0.
Note
The default convention is to interpret this value as decimal degrees. To specify radians instead, follow the value with the "r" character.
Example: +lon_0=1.570796r
See Projection Units for more information.
- +x_0=<value>¶
False easting, easting at false origin or easting at projection centre (naming and meaning depend on the projection method). Always in meters.
Defaults to 0.0.
- +y_0=<value>¶
False northing, northing at false origin or northing at projection centre (naming and meaning depend on the projection method). Always in meters.
Defaults to 0.0.
- +R=<value>¶
Radius of the sphere, given in meters. If used in conjunction with
+ellps,+Rtakes precedence.See Ellipsoid size parameters for more information.
Mathematical definition¶
The formulas describing the Tobler-Mercator are taken from Waldo Tobler's article [Tobler2018]
Spherical form¶
For the spherical form of the projection we introduce the scaling factor: