Mercator¶
The Mercator projection is a cylindrical map projection that origins from the 16th century. It is widely recognized as the first regularly used map projection. It is a conformal projection in which the equator projects to a straight line at constant scale. The projection has the property that a rhumb line, a course of constant heading, projects to a straight line. This makes it suitable for navigational purposes.
Classification |
Conformal cylindrical |
Available forms |
Forward and inverse, spherical and ellipsoidal |
Defined area |
Global, but best used near the equator |
Alias |
merc |
Domain |
2D |
Input type |
Geodetic coordinates |
Output type |
Projected coordinates |
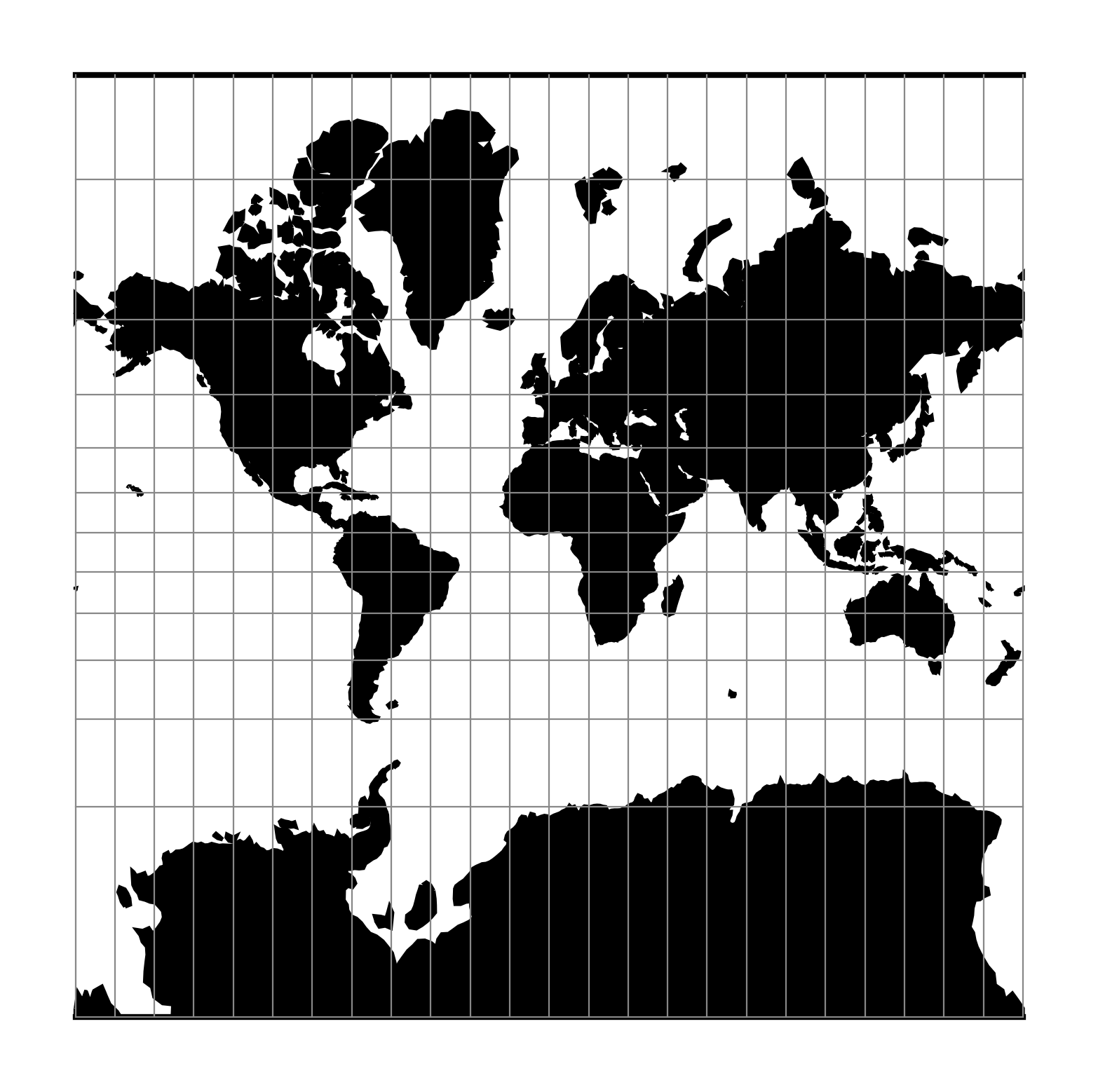
proj-string: +proj=merc¶
Usage¶
Applications should be limited to equatorial regions, but is frequently
used for navigational charts with latitude of true scale (+lat_ts) specified within
or near chart’s boundaries.
It is considered to be inappropriate for world maps because of the gross
distortions in area; for example the projected area of Greenland is
larger than that of South America, despite the fact that Greenland’s
area is \(\frac18\) that of South America [Snyder1987].
Example using latitude of true scale:
$ echo 56.35 12.32 | proj +proj=merc +lat_ts=56.5
3470306.37 759599.90
Example using scaling factor:
echo 56.35 12.32 | proj +proj=merc +k_0=2
12545706.61 2746073.80
Note that +lat_ts and +k_0 are mutually exclusive.
If used together, +lat_ts takes precedence over +k_0.
Parameters¶
Note
All parameters for the projection are optional.
- +lat_ts=<value>¶
Latitude of true scale. Defines the latitude where scale is not distorted. Takes precedence over
+k_0if both options are used together.Defaults to 0.0.
- +k_0=<value>¶
Scale factor. Determines scale factor used in the projection.
Defaults to 1.0.
- +lon_0=<value>¶
Longitude of projection center.
Defaults to 0.0.
- +x_0=<value>¶
False easting.
Defaults to 0.0.
- +y_0=<value>¶
False northing.
Defaults to 0.0.
- +ellps=<value>¶
The name of a built-in ellipsoid definition.
See Ellipsoids for more information, or execute
proj -lefor a list of built-in ellipsoid names.Defaults to “GRS80”.
- +R=<value>¶
Radius of the sphere, given in meters. If used in conjunction with
+ellps,+Rtakes precedence.See Ellipsoid size parameters for more information.
Mathematical definition¶
Spherical form¶
For the spherical form of the projection we introduce the scaling factor:
Forward projection¶
The quantity \(\psi\) is the isometric latitude.
Inverse projection¶
Ellipsoidal form¶
For the ellipsoidal form of the projection we introduce the scaling factor:
where
\(a\,m(\phi)\) is the radius of the circle of latitude \(\phi\).
Forward projection¶
Inverse projection¶
The latitude \(\phi\) is found by inverting the equation for \(\psi\). This follows the method given by [Karney2011tm]. Start by introducing the conformal latitude
The tangents of the latitudes \(\tau = \tan\phi\) and \(\tau' = \tan\chi = \sinh\psi\) are related by
where
This is obtained by taking the \(\sinh\) of the equation for \(\psi\) and using the multiple argument formula. The equation for \(\tau'\) can be solved to give \(\tau\) using Newton’s method using \(\tau = \tau'/(1 - e^2)\) as an initial guess and with the needed derivative given by
This converges after no more than 2 iterations. Finally set \(\phi=\tan^{-1}\tau\).